Optimizer

For temporary use.

SGD

• Multi-dimension function's gradient is perpendicular to tangent plane.
  • Proof1
  • Proof2
  • 1d function's derivative is gradient and has no plane.
  • In a cross section, gradient is perpendicular to derivative:
• Going downhill reduces the error, but the direction of steepest descent most likely does not point at the minimum(zig-zag). If ellipse is a circle, the direction definitely points to the minimum.

• Magnitude of gradient and curvature decide the max drop of error.

• GD: sum of loss of all examples
• SGD: one example a time to add randomness
• Mini batch SGD: to save speed and add randomness

references

• csc321
• GD
• csc2535

Momentum

Problem: pathological curvature

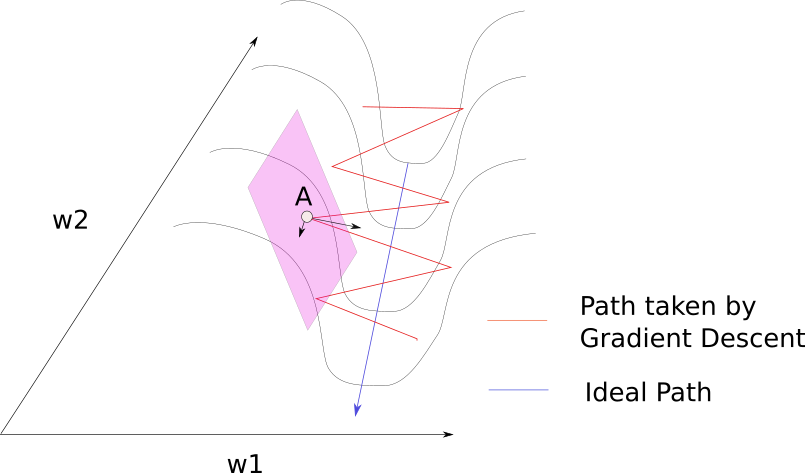
We want to slow down the speed along w1, but speed up along w2, as minimum is towards w2

Newton's method: hessian matrix

$H(e)=\left[\begin{array}{cccc} \frac{\partial^{2} e}{\partial w_{1}^{2}} & \frac{\partial^{2} e}{\partial w_{1} \partial w_{2}} & \cdots & \frac{\partial^{2} e}{\partial w_{1} \partial w_{n}} \\ \frac{\partial^{2} e}{\partial w_{2} \partial w_{1}} & \frac{\partial^{2} e}{\partial w_{2}^{2}} & \cdots & \frac{\partial^{2} e}{\partial w_{2} \partial w_{n}} \\ \vdots & \vdots & & \vdots \\ \frac{\partial^{2} e}{\partial w_{n} \partial w_{1}} & \frac{\partial^{2} e}{\partial w_{n} \partial w_{2}} & \cdots & \frac{\partial^{2} e}{\partial w_{n}^{2}} \end{array}\right]$

• learning step is inversely proportional to curvature(how quickly the surface is getting less steeper).
• hessian decides curvature

Momentum

moving_avg = alpha * moving_avg + (1 if no dampening else 1-alpha) * (w.grad)
w = w - lr * moving_avg

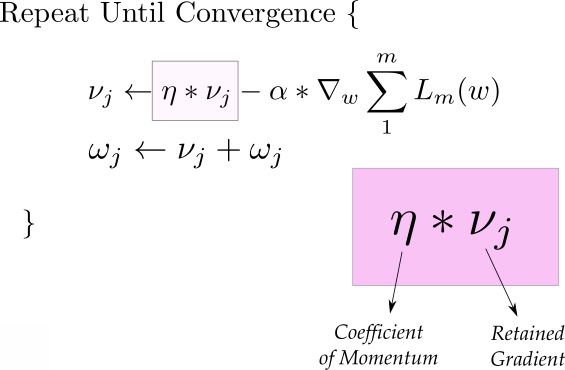
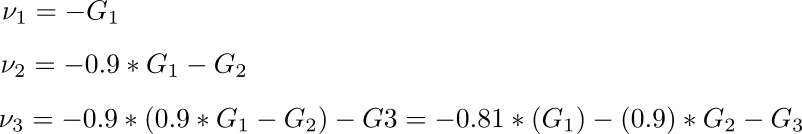
• most recent gradient matters more
• gradient history takes account, some redundant zig-zag canceled out.

references

Momentum

RMSProp

root mean square propagation

• most recent gradient matters more
• larger w, smaller step (ita divided by velocity)
• as training continues, velocity grows larger and thus steps becomes smaller when near to minimum
• epsilon is used to avoid division by zero
• adaptive: calculation for each weight separately and steps are changed automatically(not ita)

Adam

for t in range(num_iterations):
    avg_grads = beta1 * avg_grads + (1-beta1) * w.grad
    avg_squared = beta2 * (avg_squared) + (1-beta2) * (w.grad ** 2)
    avg_grads_hat = avg_grads / (1 - np.power(beta_1, t))
    avg_squared_hat = avg_squared / (1 - np.power(beta_2, t))
    w = w - lr * avg_grads_hat / sqrt(avg_squared_hat)

Weight decay

We will still use a lot of parameters, but we will prevent our model from getting too complex. This is how the idea of weight decay came up. One way to penalize complexity, would be to add all our parameters (weights) to our loss function. Well, that won’t quite work because some parameters are positive and some are negative. So what if we add the squares of all the parameters to our loss function. We can do that, however it might result in our loss getting so huge that the best model would be to set all the parameters to 0.

To prevent that from happening, we multiply the sum of squares with another smaller number. This number is called weight decay or wd.

1. l2 regularization: adding wd*w to the gradients

   final_loss = loss + wd * all_weights.pow(2).sum() / 2
   

2. weight decay: minus wd*w at the end, used by AdamW

   w = w - lr * w.grad - lr * wd * w
   

L2 regularization ≠ weight decay in complex optimizer like Adam (they are equal in SGD)

references

• Adam
• AdamW
• Weight decay